#351 - Difficult Number Series
Find the next number in the series ?
1 10 24 43 67 ?
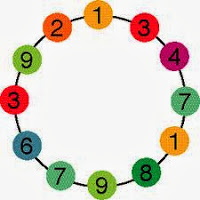
96
Difference between two numbers are
9,14,19,24,29.
Difference between every consecutive number is 5.
So next number is 67+29=96
#353 - Classic 13 Cave Logic Riddle
13 caves are arranged in a circle at the temple of doom. One of these caves has the treasure of gems and wealth. Each day the treasure keepers can move the treasure to an adjacent cave or can keep it in the same cave. Every day two treasure seekers visit the place and have enough time to enter any two caves of their choice.
How do the treasure seekers ensure that they find the treasure in minimum possible days ?
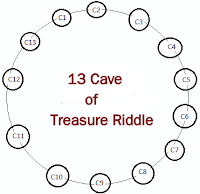
If one of the treasure seeker moves clockwise every day and one of the treasure seeker moves anti clockwise, they will find the treasure in minimum seven days.
#354 - Difficult Brain Twister
There are 100 bulbs in a room. 100 strangers have been accumulated in the adjacent room. The first one goes and lights up every bulb. The second one goes and switches off all the even numbered bulbs - second, fourth, sixth... and so on. The third one goes and reverses the current position of every third bulb (third, sixth, ninth… and so on.) i.e. if the bulb is lit, he switches it off and if the bulb is off, he switches it on. All the 100 strangers progresses in the similar fashion.
After the last person has done what he wanted, which bulbs will be lit and which ones will be switched off ?
Ponder over the bulb number 56, people will visit it for every divisor it has. So 56 has 1 & 56, 2 & 28, 4 & 14, 7 & 8. So on pass 1, the 1st person will light the bulb; pass 2, 2nd one will switch it off; pass 4, light it; pass 7, switch it off; pass 8, light it; pass 14, switch it off; pass 28, light it; pass 56, switch it off.
For each pair of divisors the bulb will just end up back in its preliminary state. But there are cases in which the pair of divisor has similar number for example bulb number 16. 16 has the divisors 1 & 16, 2 & 8, 4&4. But 4 is recurring because 16 is a perfect square, so you will only visit bulb number 16, on pass 1, 2, 4, 8 and 16… leaving it lit at the end. So only perfect square bulbs will be lit at the end.
#355 - Great Password Riddle
Vin Diesel is pulling a theft and has planned to run away with all the cash kept in the safe. But the only way to open the safe is the 13 character password. He has a set of five clues given to him by a trustworthy source.
Exactly two of the below statements are false.
The password is contained within this sentence.
The password is not in this hint.
The password is within only one of these statements.
At least one of the above statement is a lie.
The Password, Clues 2 and 5 are correct and rest are lies.
#356 - Mind Boggling Puzzle
It's time for a mind boggling puzzle.Analyze the statements below and find out who did it.
Please note that three of the statements below are false.
1. Mr. Reese: 'Mr. Bilbo did it.'
2. Mr. Bilbo: 'Mr. Reese did it.'
3. Mr. Gerry: 'Mr. Bilbo’s telling the truth.'
4. Mr. Yang: 'Mr. Gerry’s not lying.'
Mr. Bilbo did it.
Let us consider all the statements one by one for every person and find out.
Case 1: Mr. Bilbo did it, then
Statement 1 => true
Statement 2 => false (as Reese did not do it)
Statement 3 => false (as Mr. Bilbo is lying)
Statement 4 => false (as Mr. Gerry is lying)
It was Mr. Bilbo who did it. But let us confirm by taking up other cases as well.
Case 2: Mr. Reese did it, then
Statement 1 => false (as Mr. Bilbo did not do it)
Statement 2 => true
Statement 3 => true (as Mr. Bilbo is not lying)
Two statements are true whereas only one should be true, thus Mr. Reese did not do it.
Case 3: Mr. Gerry did it, then
Statement 1 => false (as Mr. Bilbo did not do it)
Statement 2 => false (as Mr. Reese did not do it)
Statement 3 => false (as Mr. Bilbo is lying)
Statement 4 => false (as Mr. Gerry is lying)
All four statements stand false, thus Mr. Gerry did not do it.
Case 4: Mr. Yang did it, then
Statement 1 => false (as Mr. Bilbo did not do it)
Statement 2 => false (as Mr. Reese did not do it)
Statement 3 => false (as Mr. Bilbo is lying)
Statement 4 => false (as Mr. Gerry is lying)
All four statements are false therefore Mr. Yang did not do it.
We have verified with everyone and now know that it was Mr. Bilbo who did it.
#357 - Challenging Math Equations Puzzle
We have arranged an array of numbers below. What you have to do is use any kind of mathematical symbol you know excluding any symbol that contains a number like cube root. You can use any amount of symbols but you have to come up with a valid equation for all of them.
0 0 0 = 6
1 1 1 = 6
2 + 2 + 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
(0! + 0! + 0!)! = 6
(1 + 1 + 1)! = 6
2 + 2 + 2 = 6
3 x 3 - 3 = 6
√4 + √4 + √4 = 6
5 + 5/5 = 6
6 + 6 - 6 = 6
7 - 7/7 = 6
8 - √√(8 + 8) = 6
√(9 x 9) - √9 = 6
#358 - Maths Logical Problem
Accidentally, two trains are running in the opposite direction and enter a tunnel that is 200 miles long. A supersonic bird that has fled the lab and taken shelter in the tunnel starts flying from one train towards the other at a speed of 1000 mph. As soon as it reaches the second train, he starts flying back to avoid collision and meets the first train again at the other end. The bird keeps flying to and fro till the trains collide with each other.
What is the total distance that the supersonic bird has traveled till the trains collided?
Let us consider the length of the tunnel first; which is 200 miles. Now, the trains are running on the same speed which means that they will collide at the center of the tunnel and will take an hour to reach the center. Now the bird is travelling at a speed of 1000 mph and it is flying for an hour (since the trains will take an hour to collide). Thus the bird will travel 1000 miles in the process.
#359 - Truth Lie Puzzle
Tia and Mia are twin sisters.One of them is a liar whereas the other one is a truth teller.
I called their home number and one of them picked up.
I asked. 'Does Tia lie?' The person replied with a yes.
Whom did I talk with? Tia or Mia ?
I spoke with Mia.
Let us assume that Tia is a liar and Mia is a truth teller.
If I asked the question from Mia, the answer will be yes. If I asked the question from Tia, the answer will be no. Thus I must have asked from Mia.
Let us assume that Tia is a truth teller and Mia is a liar.
If I asked the question from Mia, the answer will be yes. If I asked from Tia, the answer will be no. Thus in this case as well, I must have asked from Mia.
#360 - Hard Count Number Triangles Puzzle
Can you count the number of triangles on the puzzle below.
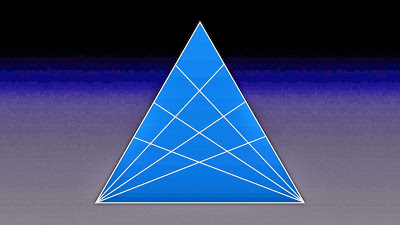
64