#721 - Replace Shape Puzzle
Can you replace the X (both small and big x) with the numbers between 1 to 19 such that all the rows of 3 numbers between X (big x) sum to 23 ?

Can you replace the X (both small and big x) with the numbers between 1 to 19 such that all the rows of 3 numbers between X (big x) sum to 23 ?

Can you replace each alphabet with the number (1 - 9) to make below equation correct ?
AB * C = DE - F = GH / I
39 * 1 = 45 - 6 = 78 / 2
AB - C = DE / F = GH * I can be solved as
A = 3
B = 9
C = 1
D = 4
E = 5
F = 6
G = 7
H = 8
I = 2
So below equation can be solved as:
AB - C = DE / F = GH * I
39 * 1 = 45 - 6 = 78/2
39 = 39 = 39.
Josh Parker organizes an exotic office Christmas party at the beach to his important fellow employees.
Following are the important people that will come to the party
1. Josh Parker
2. Josh Parker 2 girlfriends- Carol Vanstone and Tracey Hughes
3. The sales head Clay Vanstone.
4. Clay Vanstone 2 associates.
5. Mr. Jeremy and his Secret Tab.
They all need to cross a small river to reach the beach, however, Josh Parker has got just one boat.
There are few rules for crossing the river.
1. The capacity of the boat is limited to just two people.
2. Clay Vanstone associates will not stay with Josh Parker without Clay Vanstone.
3. Carol Vanstone and Tracey Hughes will not stay with the Clay Vanstone without Josh Parker.
4. Mr. Jeremy would never leave the Secret Tab alone.
5. Secret Tab counts as a person.
6. Only Josh Parker, Clay Vanstone or Mr. Jeremy can drive the boat.
7. The two girlfriends Carol Vanstone and Tracey Hughes will not stay with the Clay Vanstone without Josh Parker.
8. No Associates would stay with Josh Parker without their Clay Vanstone.
9. Mr.Jeremy will not leave the Secret Tab alone.
1. Mr.Jeremy and girlfriend1, Mr.Jeremy back
2. Mr.Jeremy and girlfriend2, Mr.Jeremy back
3. Clay Vanstone and Josh Parker, Clay Vanstone back
4. Mr.Jeremy and Secret Tab, Mr.Jeremy back
5. Mr.Jeremy and Clay Vanstone, Mr.Jeremy back
6. Mr.Jeremy and associate1, Mr.Jeremy back
7. Mr.Jeremy and associate2.
Can you solve below alphametic riddle by replacing letters by number to make below equation true ?
NUMBER +
NUMBER
=======
PUZZLE
It can be solved as shown below.
201689 +
201689
-------
403378
There are three boxes which are labeled as Rs100, Rs150, and Rs200. One box contains two notes of Rs. 50. The second box contains one note of Rs50 and one note of Rs100 The third box contains two Rs. 100 notesAll boxes are labeled incorrectly.
What is the minimum number of boxes you must check in order to label all boxes correctly?
You just need to check Rs.150 box.
Explanation: The trick to solving this puzzle is to remember that all boxes are labeled incorrectly.
Case 1: If it contains Rs. 100 notes, then
A) Current box contains Rs. 200 notes.
B) Rs 100 box contains Rs. 150 notes.
C) Rs. 200 box contains Rs. 100 notes.
Case 2: If it contains Rs. 50 notes, then
A) Current box contains Rs. 100 notes.
B) Rs. 100 box contains Rs. 200 notes.
C) Rs. 200 box contains Rs. 150 notes.
Can you replace alphabets by the numbers to make all the below equations true?
ZY = XZ - WV
UT = YV - ST
WY = ZU - RZ
QX = PX - QV
QL = LQ - WP
SV = XT - YR
Note: You can using only 8 digits. (i.e. more than one alphabets will be mapped to same numerical value)
Z = Y = P =6
X =7
W = S = 1,
V=0 ,
U = R = T = 4,
Q=3,
L=5
Now we can rewrite the equations as :
66 = 76 - 10
44 = 60 - 14
16 = 64 - 46
37 = 67 - 30
35 = 53 - 16
10 = 74 - 64
Can you quickly find which two matchstick figures is identical?
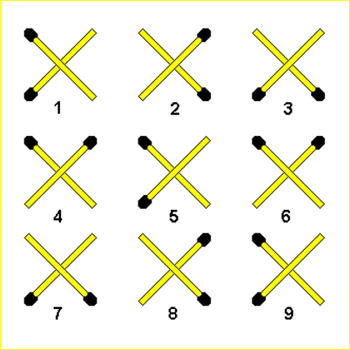
5 and 9
Jigsaw captured 100 people and make them stand in the circle and all these people are labeled as Person1, Person2, Person3... Person100. He made them play a crazy game in which the Person1 shot the Person2 and pass the gun to next Person and so on until one stands alive.
Which person will survive at the end?
73
Below rebus represent famous DiCaprio movie. Can you name it?>br>

Catch Me If You can
"Cat" + "ch" (China - Ina) + "Me" (Me icon) + If (Gif icon - G, we removed G as 1 is cut off) + "You" (it is pointing towards You) + Can (picture of can)