#121 - Find The Thief Riddle
Can you find the thief by just looking at the picture below?
The Lady sitting in the chair has the detector attached to the back of her blouse.
#122 - Missing Rs1 Puzzle
I have Rs.50 and i spend in the way below.
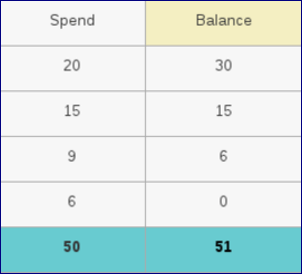
Adding commutative balance does not make any sense.
Check my next example, where is spend Rs 50 in way below
Spent Balance
10 40
10 30
10 20
10 10
10 0
==============
50 100
So in the puzzle, the number was chosen to confuse readers.
#123 - Good Age Riddle
Lena Dunham , Allison Williams, and Jemima Kirke are 3 daughters of a good mathematician "Geroge".
When I asked George the age of their daughters. He replied "The current age of her daughters is prime. Also, the difference between their ages is also prime."
How old are the daughters ?
Lena Dunham : 2 , Allison Williams : 5 and Jemima Kirke : 7
Age diff : 7-2 is 5 , 7-5 is 2 and 5-2 is 3 which all are prime numbers
#124 - Popular Logical Barrel Puzzle
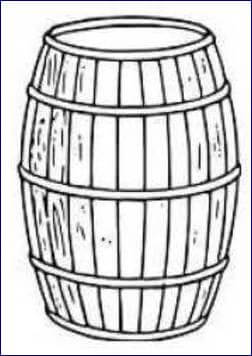
We have shown you a regular water barrel. Without using any measuring device can you check if barrels is more than half filled or less than half filled ?
Simple science, Tilt the barrel until the water will touch the upper end of the barrel. and if bottom part is visible then it is less than half filled else more than half.
#125 - Famous 10 Castles Puzzle
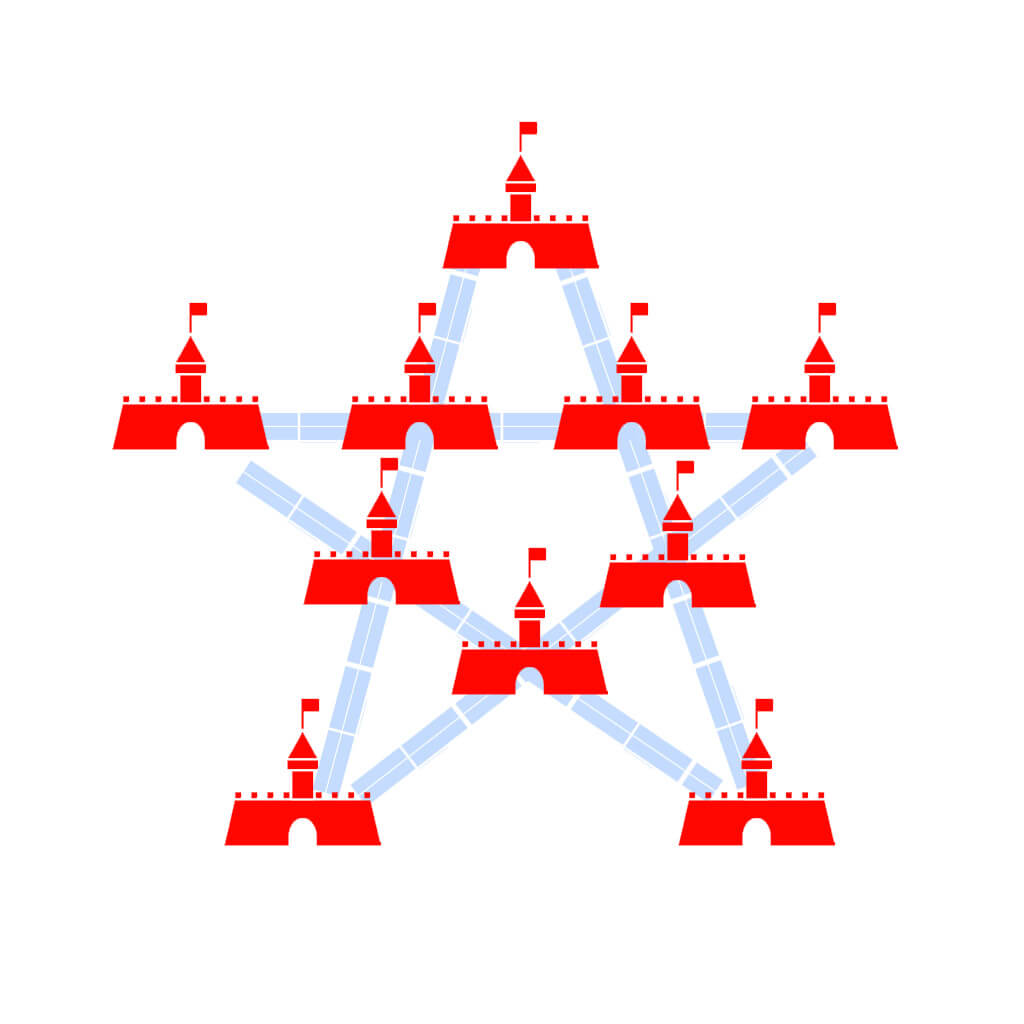
In a time long back, there lived a king who ruled the great kingdom of Trojan House. As a part of the renovation of the kingdom to meet future security needs, he asked his chief architect to lay down a new play in a manner that all of his 10 castles are connected through five straight walls and each wall must connect four castles together.He also asked the architect that at least one of his castle should be protected with walls.The architect could not come up with any solution that served all of King’s choice, but he suggested the best plan that you can see in the picture.Can you find a better solution to serve the king’s demand?
If you see the solution picture, you will find out that two castles are protected with walls in this formation.
#126 - Hard Prison CupCakes Riddle
Bea Smith , Vera Bennett, Franky Doyle and Doreen Anderson were in Wentworth Prison for murder. But their behavior on the jails is appreciated by the warden and the warden decided to give all these 4 prisoners 11 cupcakes.They all like cupcakes and they had all cupcakes in no matter of time but they do not know how many cupcake each individual had.Therefore Bea started the conversation Bea : "Hey T-Vera, did you had more cupcakes than I had ?"Vera : "I do not know girl, Hey Franky, did you had more cupcakes than I had ?".Franky: "I do not know"Doreen replied instantlyDoreen: "I know how exactly how many cupcakes each of you had?"So can you tell how many cupcakes each of them had ?
Bea : 1 cupcake
Vera : 2 cupcakes
Franky: 3 cupcakes
Doreen : 5 cupcakes
It is obvious if the prisoner person has eaten five or more of cupcakes than she wound not raise this question "did you had more cupcakes than me?" because it will make her the one who had eaten most cupcakes.
* Bea must do not have eater 5 cupcakes, therefore she has eaten anywhere between 1-4 cupcakes.
* Since Bea asked her the question Vera knows the fact that Bea has eaten 1-4 cupcakes and based on Vera reply, it is obvious she has eaten 2-4 cupcakes.
* Franky knows Vera replied with the answer as "I do not know and based on above logic, she must have had 3 or 4 cupcakes.
* Doreen replied she know all, which indicates she must have eaten 5.
#127 - Square Root 12345678987654321 Puzzle
The square root of number 121 is "11". What is the square root of number "12345678987654321." ?
111111111
It is a very popular square root series i.e.
Square root fo number 121 is 11
Square root fo number 12321 is 111
Square root fo number 1234321 is 1111 and so on....
#128 - Fill The Tank Riddle
Which tank will fill first?
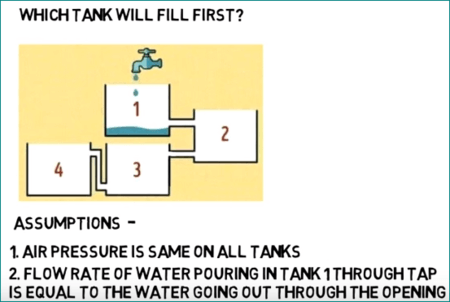
3rd and 4th.Let us break down the problem into 5 steps.1. The water in tank1 will get filled up to the connectivity of tank1 and the tank2 and then it will start flowing to tank2.2. The water in tank2 will get filled up to the connectivity of tank2 and the -tank3 and then it will start flowing to tank3.3. The water in tank3 will get filled up to the connectivity of tank2 and the tank3 and then it will start flowing to tank3.4. As the outlet of tank3 and inlet of tank4 are not at the same level, water will continue to fill tank3 till the inlet of tank4.5. Now both the tank3 and tank4 fill simultaneously until both fill together.
#129 - The Cards Magic Riddle
David Blaine and Dynamo performed together in our college fest. I was chosen to be performed a card trick on. Blaine asked me to shuffle a deck of cards and when I was done, he asked me to pick any five cards. I did as he had asked and showed my selected cards to Blaine. Out of those five cards, he gave four to Dynamo and one back to me. Upon looking at those four cards, he was able to deduce the card I was holding. I was shocked. It was brilliant. But when I was returning back home, I thought about it and was able to crack the trick. Do you know how they did it?
It is plain and simple that in five cards, two cards must be of the same suit.
What Blaine did was place one of those cards at the end and gave the other cards to Dynamo. Now, Dynamo knows the suit of the card.
So how did Blaine ensure that Dynamo knows the number on the card as well?
Since one of the cards determines the suit, we have 3 cards. If you know a little about permutations, the 3 cards can be arranged in 3! ways i.e. 6 ways. If we make sure that the King is not picked, it leaves us with just 12 numbers.
The cards can be distinguished from upside down position, which gives us 6*2 ways of arranging the cards.
Let us denote the smallest card as X1U for upward position and X1D for the downward position. We can go up from there as X2U, X2D, X3U, X3D and so on.
The possible 12 arrangements will now be
X1U X2U X3U => Card No. 1
X1U X3U X2U => Card No. 2
X2U X1U X3U => Card No. 3
X2U X3U X1U => Card No. 4
X3U X1U X2U => Card No. 5
X3U X2U X1U => Card No. 6
X1D X2D X3D => Card No. 7
X1D X3D X2D => Card No. 8
X2D X1D X3D => Card No. 9
X2D X3D X1D => Card No. 10
X3D X1D X2D => Card No. 11
X3D X2D X1D => Card No. 12
#130 - Number Dot Algebric Riddle
Can you solve the below algebraic picture puzzle?
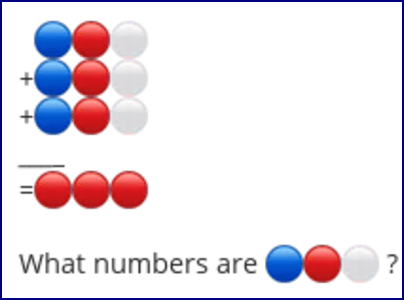
1 8 and 5 (185+185+185 = 555)