#11 - Maths Equation Operator Puzzle
I know there are two methods by using three time the same number with an plus(+) operator , you can make sum as 60.
One of them is 20+20+20.
whats the other way ?
The Other way is 55+5
#12 - Solve Maths Equation Problem
Find the value of a by solving the maths equation in the picture below
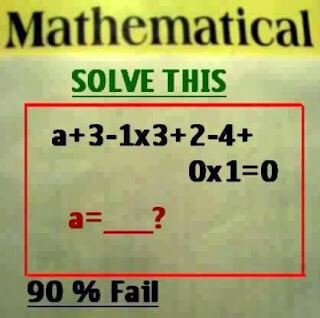
2(remember bodmas)
#13 - Logical Maths Picture Puzzle
Solve the maths equation in the picture below by placing the numbers 1 through 9 into the boxes so that all the 3 equations are correct.
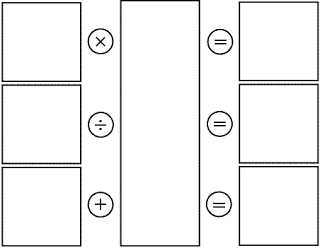
There are six unique answers
Ans1:
7 x 4 = 28
36 / 4 = 9
1 + 4 = 5
Ans2:
9 x 4 = 36
28 / 4 = 7
1 + 4 = 5
Ans3:
3 x 8 = 24
56 / 8 = 7
1 + 8 = 9
Ans4:
7 x 8 = 56
24 / 8 = 3
1 + 8 = 9
Ans5:
4 x 8 = 32
56 / 8 = 7
1 + 8 = 9
Ans6:
7 x 8 = 56
32 / 8 = 4
1 + 8 = 9
#14 - Challenging Math Equations Puzzle
We have arranged an array of numbers below. What you have to do is use any kind of mathematical symbol you know excluding any symbol that contains a number like cube root. You can use any amount of symbols but you have to come up with a valid equation for all of them.
0 0 0 = 6
1 1 1 = 6
2 + 2 + 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
(0! + 0! + 0!)! = 6
(1 + 1 + 1)! = 6
2 + 2 + 2 = 6
3 x 3 - 3 = 6
√4 + √4 + √4 = 6
5 + 5/5 = 6
6 + 6 - 6 = 6
7 - 7/7 = 6
8 - √√(8 + 8) = 6
√(9 x 9) - √9 = 6
#15 - Hard Number Riddle
Can you find out the smallest number that can be conveyed as the sum of three squares in three unique ways ?
54
7^2 + 2^2 + 1^1
6^2 + 3^2 + 3^2
2^2 + 5^2 + 5^2
#16 - Hard Maths Equation Problem
In a mathematical quiz, you are asked the following question:
Use three 9's in a mathematical expression without dividing or multiplying in order to form the number one.
Can you answer the question?
The answer is 9^(9-9)
#17 - Trick Equation Problem
The following equation can be made correct by moving one small line. Can you find out how?
6 + 6 + 2 = 34034
Move one line from the plus sign and place it on the RHS as shown.
6 + 6 - 2 = 340/34
#18 - Mathematical Proof Puzzle
Below, you will find the mathematical proof that 10 equals 9.99999…. But is that possible or there is something wrong about it? Can you find the error?
x = 9.999999...
10x = 99.999999...
10x - x = 90
9x = 90
x = 10
No error is present in this proof and 10 is actually equal to 9.99999…. The proof is absolutely correct.
#19 - Matchstick Equation Puzzle
An equation has been laid down using a few matchsticks. However, as you can see, the equation is not correct. Can you correct the equation if you are allowed to add or remove 5 matchsticks?
As you can see in the answer figure, the equation stands true now. Compare the images to know what we have done.
#20 - Complete The Equation Puzzle
Below, you can see three complete equations and one incomplete. Based on the three complete ones, can you complete the incomplete one?
5 $ 4 $ 3 $ 9 = 4215
6 $ 9 $ 2 $ 6 = 3816
4 $ 7 $ 3 $ 3 = 1122
7 $ 2 $ 7 $ 4 = ____
2418 is the answer.
The algo that has been used here is
A $ B $ C $ D = [first digit of (A * D)] [last digit of (B * C)] [first digit of (B * C)] [last digit of (A * D)]
Using the same algo,
7 $ 2 $ 7 $ 4 = [first digit of (7 * 4)] [last digit of (2 * 7)] [first digit of (2 * 7)] [last digit of (7 * 4)]
= 2418