#671 - Strange Birthday Puzzle
Today, I celebrated my 32nd birthday but I was born in 1971.
How is this possible ?
I was born in Hospital whose room number is 1971.
Today, I celebrated my 32nd birthday but I was born in 1971.
How is this possible ?
I was born in Hospital whose room number is 1971.
This is the interview puzzle asked to my friend in an interview of "blackrock".
As shown in the picture below, There is a circular car race track of 10km. There are two cars, we called them Car A and Car B. And they are at the exact opposite end to each other. At Time T(0), Both cars move toward each other at a constant speed of 100m / seconds. As we know both cars are at the same speed they will always be the exact opposite to each other.
Note, at the center, there is a bug which starts flying towards Car A at time T(0). When the bug reaches car B, it turns back and starts moving towards the car A. The speed of bug is 1m/second. After 5hours all three stop moving.
What is the total distance covered by the bug?
As we know bug travels at a constant speed of 1m/seconds
=> in 5 hours
=> 5 * 60 * 60 meters
=> 18km.
Can you complete below number series by replacing "?" with the correct number.
10 # 10 # 20 # ? # 110 # 300 # 930
45
Pattern goes like
10
10 * 0.5 + 5 => 10
10 * 1.0
+ 10 => 20
20 * 1.5 + 15 => 45(Ans)
45 * 2.0 + 20 => 110
110 * 2.5 + 25 => 300
300 * 3.0 + 30 => 930
A mother bought three dress for her triplets daughters(one for each) and put the dresses in the dark. One by one the girls come and pick a dress.
What is the probability that no girl will choose her own dress?
1/3
Explanation
Assuming D1 is the dress for Sister1, D2 is the dress for Sister2 and D3 is the dress for Sister3.
Therefore the total number of cases are illustrated below.
Sister1 Sister2 Sister3
D1 D2 D3
D1 D3 D2
D2 D1 D3
D2 D3 D1 ..... (1)
D3 D1 D2 .... (2)
D3 D2 D1
In both steps (1) & (2), no one gets the correct Dress.
Therefore probability that no sister gets the correct dress is 2/6 = 1/3
This is a hardest chess board puzzle that I have been asked.In the picture below you can see that white army is arranged. You need to add black army in the board such that no piece is under any threat.Note: Army comprised of 1 king 1 queen 2 rooks 2 bishops 2 knights 8 pawns

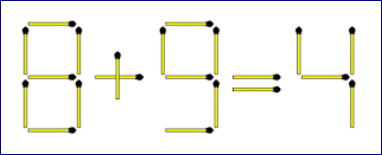
By moving exactly three matchsticks can you make the below equation true.It can be solved by 3 ways.
By using all numbers, i.e. 123456789 and subtraction/addition, operators number 100 can be formed in many ways.
Example 98 + 7 + 6 - 5 - 4 - 3 + 2 - 1 = 100
But if we add a condition that use of the number 32 is the must. Then there are limited solutions.
One of such solution is: 9 - 8 + 76 + 54 - 32 + 1 = 100
Can you tell any other solution?
9 - 8 + 7 + 65 - 4 + 32 - 1 = 100
9 - 8 + 76 + 54 - 32 + 1 = 100
Other ways of making number 100 (withiout using number 32)
98 + 7 + 6 - 5 - 4 - 3 + 2 - 1 = 100
98 - 7 - 6 - 5 - 4 + 3 + 21 = 100
9 - 8 + 76 - 5 + 4 + 3 + 21 = 100
98 - 7 + 6 + 5 + 4 - 3 - 2 - 1 = 100
98 + 7 - 6 + 5 - 4 + 3 - 2 - 1 = 100
98 + 7 - 6 + 5 - 4 - 3 + 2 + 1 = 100
98 - 7 + 6 + 5 - 4 + 3 - 2 + 1 = 100
98 - 7 + 6 - 5 + 4 + 3 + 2 - 1 = 100
98 + 7 - 6 - 5 + 4 + 3 - 2 + 1 = 100
98 - 7 - 6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 - 3 + 2 - 1 = 100
9 + 8 + 76 + 5 - 4 + 3 + 2 + 1 = 100
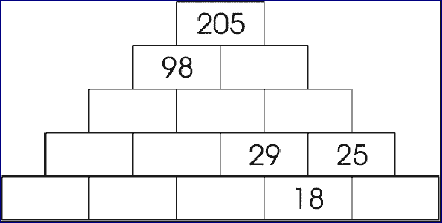
You need to fill number in the bricks in the image below such that the top brick is sum of two brick below it.