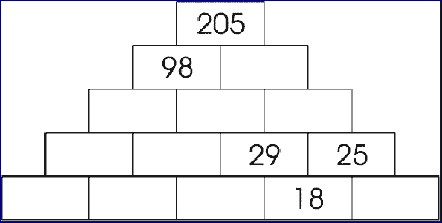
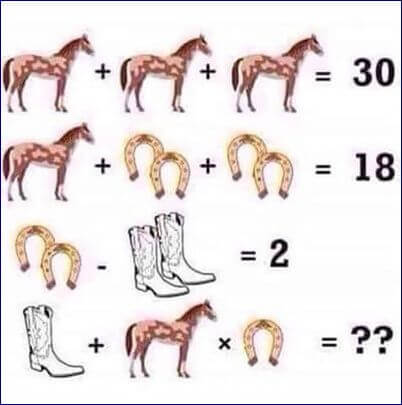#121 - Good Equation Riddle
Is it possible to get ten whether you remove one from nine or eleven? How?
It is possible if you write numbers in their roman forms.
11 = XI
If I (1) is removed, it becomes X = 10
9 = IX
If I (1) is removed, it becomes X = 10