#241 - Rebus Math Riddle
What does this maths rebus means ?
absolutely not
#242 - Solve Mathematical Problem
There are two insects on a tile. Insect X is sitting on one side of the tile (point A) and Insect Y is sitting opposite on the other side of the tile (point B). Now both of them decide to change their position and thus X starts crawling to point B and Y starts crawling to point A. When they meet and pass each other in between, X takes 20 seconds to reach to B and Y takes just 5 seconds to reach A.
Can you calculate the total time each of the insects took to change their positions?
Assume that P is the speed of Insect X and Q is the speed of Insect Y.
Let T be the number of seconds it takes them to cross paths.
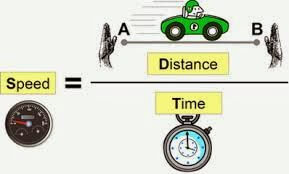
Now Distance = Speed * Time
Thus for Insect X
Distance = P * T before meeting
And Distance = P *20 after meeting
For Insect Y
Distance = Q * T before meeting
And Distance = Q * 5 after meeting
Now the distance travelled by X before meeting is equal to the distance travelled by Y after meeting and vice versa
Thus
P * T = Q * 5
And Q * T = P * 20
Solving both equations, we get T = 10
Thus Insect X requires 10 + 20 = 30 seconds,
Whereas Insect Y requires 10 + 5 = 15 seconds to change the position.
#243 - Hard Mathematics Expression Puzzle
You are given with six numbers – 1, 2, 3, 4, 5 and 6. You can arrange them in any order and you can use all the four mathematics expression i.e. add, subtract, multiply and divide and also parenthesis. The result must be 278.
There are three other rules
1) You can only use a number once.
2) It is not compulsory to use all the six numbers.
3) You can't join numbers i.e. you can't use 1, 2 and 3 as 123.
(1 + (3 + 4*5)*6)*2
There can be more than one possibilities.
#244 - Math Figure Puzzle
An exterior architect is asked by a builder to plant seven trees in a manner that there are exactly six rows of trees in a straight line and each row has three trees in particular.
How will he do it?
He will plant three trees as the vertices of an equilateral triangle. Now imagine an equilateral triangle. Three more trees will be planted on the center of each of the side of the triangle. The remaining one tree will be planted at the centroid of the hypothetical equilateral triangle.
#245 - Math Logic Problem
In a modern art gallery, an artist has numerous modern art paintings created by him. He hangs different painting on the space provided to him periodically. When the clock hit 11 am, he hung the painting number 30. When it struck 4 pm, he hung the painting number 240 and when it struck 7:30 pm, he hung painting number 315.
Can you determine, which painting number will he hang when the time is 9:20 pm ?
He will hang painting number 200 at that time. Every time he hangs the painting, the number of it corresponds with the angle between the minute and hour hand of the clocks.
#246 - Tricky Maths Puzzle
A train leaves from point A for point B at 80 mph. After half an hour, another train leaves from point B for point A at 60 mph.
Which of the trains will be further from point A when they meet ?
When the trains meet, they will be approximately be equally distant from point A. Of course if you get into precise details, the train that left from point A will be closer to A by its own length as they are coming from different directions.
#247 - Hard Math Question
A generous owner of a company decided to give a bonus of $45 to every man and $60 to every woman on his birthday. But only one ninth of the men and one twelfth of woman were present to take the bonus.
Can you calculate the amount of money the owner spent if there were 3552 employees ?
17,760
Let us assume that there are x male employees.
No. of female employees will be (3553 – x)
One ninth of men = x/9 who received $45
And one twelfth of the women = (3553 – x) /12 who received $60
Thus total received = (45 * (x / 9)) + (60 * (3552 - x) / 12)
= 5 * 3552
= $17,760
#248 - Hard Maths Logic Question
There is a jar in which there are two types of candies – 20 blueberry and 16 strawberry. You perform the following steps:
1) You take out two candies.
2) If the two candies are of same flavor, you add a blueberry one otherwise, you add the strawberry one.
You repeat these two steps till there is just one candy remaining in the jar. Which flavored candy will be left?
Also, if you began with 100 blueberry candies and 93 strawberry candies, which flavor would have been the last one to remain?
Let us suppose that there are x blueberry candies and y strawberry candies. While removing the candies, there can be three possibilities:
1) 2 blueberry candies. In this case, you will replace one blueberry candy and so the jar will have x+1 blueberry and y-2 strawberry candies.
2) 2 strawberry candies. In this case, you will replace 1 blueberry candy and so the jar will have x-1 blueberry candies and y strawberry candies.
3) 1 blueberry and 1 strawberry. In this case, you will replace a strawberry candy and so the jar will have x-1 blueberry candies and y strawberry candies.
In this way at each step, we are either removing a blueberry candy or replacing 2 strawberry candies by 1 blueberry candy irreversibly till there is only one candy left. Thus each strawberry candy is equivalent to 2 blueberry candies.
Therefore, if there are odd number of strawberry candies, the last candy will be strawberry and if there are even number of strawberry candies, the last one will be a blueberry one.
#249 - Distance Speed Problem
A car M starts from point A and a car N starts from point B and move towards opposite sides at a constant speed. The cars meet 500 yards from A for the first time. After reaching the opposite points, each of the car returns back without any break and this time, they meet 300 yards from B.
What is the distance between the two points A and B and what is the relation between the speeds of the two boats?
When the cars first meet, they have traveled a combined distance equal to the 1 length of the distance. When they meet the second time, they have travelled 3 lengths.
The elapsed time and distance for each of the cars is three times. Now when they meet the second time, M has traveled 500x3 = 1500 yards and since, it is 300 yards longer than the total distance between both the points, the distance is 1200 yards.
The ratio of M’s speed to the ratio of N’s speed is equal to the distance that they traveled before they met for the first time.
i.e. 500/(1200 – 500) = 5/7
#250 - Solve My Maths Problem
There has been a house on fire. The fireman is now standing in the middle rung of the ladder and trying to extinguish the fire. He climbs 6 rungs more but the heat and deadly flames make him climb down 10 rungs. When the fire is settling gradually, he climbs 18 rungs and reaches the top of the ladder for better access to the house.
Calculate the number of rungs in the ladder ?
29 rungs
Suppose he is standing on m at first which is the middle rung.
He climbs 6 rungs which makes his position to be m+6.
He climbs down ten rungs which makes his position to be (m+6-10) = m-4
He climbs 18 rungs to reach the top t which makes his position (m-4+18) = m+14
Now, m+14 = t
Which means there are 14 rungs above the middle rung and 14 rungs below the middle rung. Counting the middle rung as well, it makes a total of 29 rungs.