#191 - Solve Mathematical Equation
Can you solve below mathematical equation ?
2^1234 - 2^1233
2^1233
#192 - Simple But Tricky Math Questions
Three cars are driving on a track that forms a perfect circle and is wide enough that multiple cars can pass anytime. The car that is leading in the race right now is driving at 55 MPH and the car that is trailing at the last is going at 45 MPH. The car that is in the middle is somewhere between these two speeds.
Right now, you can assume that there is a distance of x miles between the leading car and the middle car and x miles between the middle car and the last car and also, x is not equal to 0 or 1.
The cars maintain their speed till the leading car catches up with the last car and then every car stops. In this scenario, do you think of any point when the distance between any two pairs will again be x miles i.e. the pairs will be x distance apart at the same time ?
Not Possible
As per the question, the middle car is running right now approximately at 50 MPH. Therefore, with time, the distance between them will keep increasing by x miles every hour for a certain time. After that, it will start decreasing between the leading car and the last car till they meet.
Therefore, you will find no point where the distance between the cars is x miles again.
#193 - Cut Board Maths Picture Problem
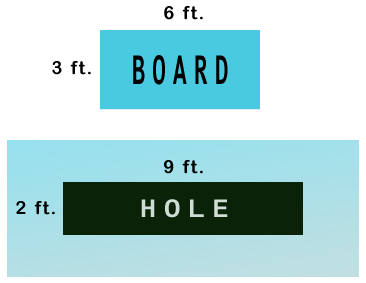
As you can see in the picture, you have a hole with dimensions 9 ft. x 2 ft. Also available to you is a wooden board with dimensions 6 ft. x 3 ft.Now you have to cover the hole with this board and you are allowed to cut the board into two pieces. Please see to it that the hole is completely covered and the boards should not be overlapping each other or extending beyond the edge.How will you cut the board?
As you can see in the picture, this is how you must cut the board and join them to cover the hole completely without leaving any gap.
#194 - Mathematics Trivia Question
Can you think of any three dimensional shape that comprises of exactly two surfaces ?
A cone comprises of exactly two surfaces despite of the fact that it is a three dimensional figure.
#195 - Tricky Math Trivia Question
Can you find out which triangle will have a bigger area among the following?
1. A triangle with sides 300, 400 and 500
2. A triangle with sides 300, 400 and 700
1st
The first option will have a bigger area. This is because the second triangle is not possible.
According to the formula:
Side 1^2 + Side 2^2 = Side 3^2
#196 - Quick Fire Maths Question
In a science lab, a petri dish hosts a healthy colony of yeast for an experiment. Now every minute, all the yeast cells divide into two. At noon, there was just a single cell of yeast and at 1:22, the Petri dish was half full. Can you calculate when the dish will be full of yeast?
Since at every minute, the cells of yeast are multiplying into two and at 1:22, the dish was half full, it will become full the very next minute i.e. at 1:23.
#197 - Difficult Math Trivia Question
Can you find out the remainder when 3^300 is divided by 5?
3
It is obvious that it is not feasible to calculate 3^300 as it will take too much of time. So we will use a trick to solve the question. We will calculate the remainder of each power till we find a pattern.
3^1 divided by 5 leaves the remainder 3.
3^2 divided by 5 leaves the remainder 4.
3^3 divided by 5 leaves the remainder 2.
3^4 divided by 5 leaves the remainder 1.
3^5 divided by 5 leaves the remainder 3.
3^6 divided by 5 leaves the remainder 4.
As you can see that the pattern is now repeating itself and it will go on like this till 3^300 and beyond. Since every fourth remainder is same as the first, we will look for the power of 4 only. 300 is divisible by 4. Therefore at the power of 300, the first remainder will repeat itself and the remainder will be 3.
#198 - GP Mathematics Puzzle
A rubber ball keeps on bouncing back to 2/3 of the height from which it is dropped. Can you calculate the fraction of its original height that the ball will bounce after it is dropped and it has bounced four times without any hindrance ?
Let us solve this question one step at a time.
We know that each time the ball is dropped it bounces back and reach 2/3 of the height.
Thus, after the first bounce, the ball will reach 2/3 of the height from which it was dropped.
After the second bounce, the ball will reach 2/3 of the height again after the first bounce.
Thus the total height at which the ball must have reached by this time will be 2/3 * 2/3 = 4/9 of the original height.
After third bounce, 2/3 * 2/3 * 2/3 = 8/27 of the original height.
After fourth bounce, 2/3 * 2/3 * 2/3 * 2/3 = 16/81 of the original height.
Thus, the ball will reach 16/81 of the original height from which it was dropped.
#199 - Here A ODI cricket riddle
here's a cricket riddle for all of cricket lovers
I have played 50 ODI's and my average is 50.
How many runs should i score in my 51st ODI, so that my average score jumps to 51 ?
101
(50 * 50 + x)/51 = 51
=>2500 + x = 51 * 51
=> x = 2601 - 2500
=> x = 101 (Answer)
#200 - Tricky Problem On Probability
There was a blind man. He had four socks in his drawer either black or white. He opened it and took out two socks. Now the probability that it was a pair of white socks is 1/2.
Can you find out the probability that he had taken out a pair of black socks ?
This question can be a tricky one. The probability that is asked will be zero.
If the probability off taking out a pair of white socks is 1/2, it means that there is no black pair. This is because if there had been, there would have been three cases – white pair, black pair and mixed pair. But since in the question it is clear that there were just two chances (1/2), we can fairly deduce that there were only one black sock and the rest were white.