#311 - Fun With Matchsticks Riddle
As we can see there are seven square in the picture below.
Can you move four match sticks to form 9 squares ?
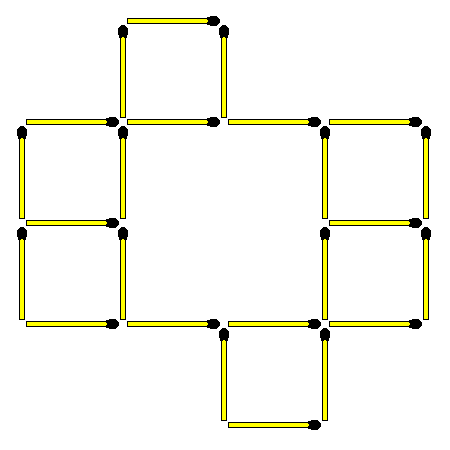
The Matchsticks Riddle can be solved as shown below.
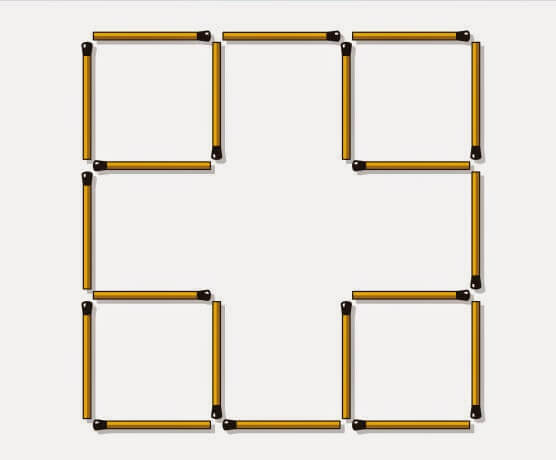
As we can see there are seven square in the picture below.
Can you move four match sticks to form 9 squares ?

The Matchsticks Riddle can be solved as shown below.
Find out the number of circles in the given picture.

There are 17 circles in this picture.
You can easily place the one in the middle. Just concentrate on that for a bit and you will know what other 16 circles are present in the picture.
As you can see in the picture, 20 matchsticks have been used to form five squares. What you have to do is move two of the matchsticks in a manner that seven squares are formed.Please note that you cannot overlap the matches or break them. The squares can be on any size but they must be closed squares.
Below puzzle is a popular example for rebus puzzles.
Can you tell us what i am thinking by solving the below rebus ?

Feeling on top of the World
Can you find the missing figure from the grid? Choose from the options given.

The figure D will fit in the missing position. This is because with every figure, the number of black dots are increasing. Thus the D figure is the only one that I suitable.
The picture shows the dice results in each couple of throws. If they are actually following a pattern, can you find out the missing one?

The last missing throw will have 3 as the result. This is because, with each pair of the throws you can find that the total sum is increasing by three and then decreasing by one. Therefore the missing throw be 3.
If you look at the figure given, you will find a square formed with match sticks. This figure comprises of five squares. Can you move the matchsticks such that the resulting figure consists of ten squares?Please note that, you can just drag the matchsticks and can’t rotate them and also you have just four moves. How will you do it?
Count the number of triangles in the given picture.
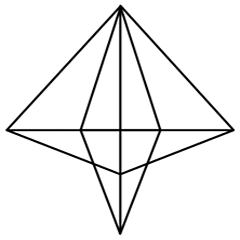
24
Just to make it easy for you to understand, we have numbered the triangles. So let us start calculating.
Ten distinct triangles numbered from 1 to 10.
Now, (1+2), (1+2), (1+2+3), (1+2+3+4), (2+3), (2+3+4), (3+4), (5+6), (5+6+7+8), (7+8), (1+2+5+6), (3+4+7+8), (2+6+9), (3+7+10), (6+9), (7+10) and (6+7+9+10).
Thus the total number of triangles are 24.