#681 - Matchsticks Equation Riddle
By moving exactly three matchsticks can you make the below equation true.It can be solved by 3 ways.
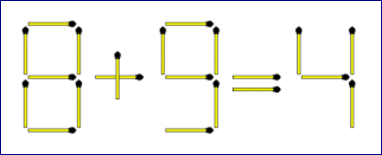
By moving exactly three matchsticks can you make the below equation true.It can be solved by 3 ways.

By using all numbers, i.e. 123456789 and subtraction/addition, operators number 100 can be formed in many ways.
Example 98 + 7 + 6 - 5 - 4 - 3 + 2 - 1 = 100
But if we add a condition that use of the number 32 is the must. Then there are limited solutions.
One of such solution is: 9 - 8 + 76 + 54 - 32 + 1 = 100
Can you tell any other solution?
9 - 8 + 7 + 65 - 4 + 32 - 1 = 100
9 - 8 + 76 + 54 - 32 + 1 = 100
Other ways of making number 100 (withiout using number 32)
98 + 7 + 6 - 5 - 4 - 3 + 2 - 1 = 100
98 - 7 - 6 - 5 - 4 + 3 + 21 = 100
9 - 8 + 76 - 5 + 4 + 3 + 21 = 100
98 - 7 + 6 + 5 + 4 - 3 - 2 - 1 = 100
98 + 7 - 6 + 5 - 4 + 3 - 2 - 1 = 100
98 + 7 - 6 + 5 - 4 - 3 + 2 + 1 = 100
98 - 7 + 6 + 5 - 4 + 3 - 2 + 1 = 100
98 - 7 + 6 - 5 + 4 + 3 + 2 - 1 = 100
98 + 7 - 6 - 5 + 4 + 3 - 2 + 1 = 100
98 - 7 - 6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 - 3 + 2 - 1 = 100
9 + 8 + 76 + 5 - 4 + 3 + 2 + 1 = 100
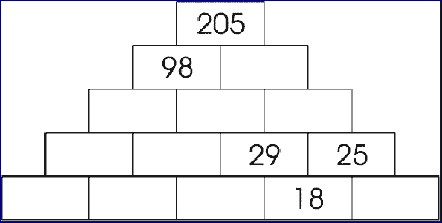
You need to fill number in the bricks in the image below such that the top brick is sum of two brick below it.
Can you find the missing number in the series below
1 5 9 2 6 10 3 ? 11 4 8 12
7
Series given in the problem :
1 5 9 2 6 10 3 ? 11 4 8 12
Let us break the series as :
1 5 9
2 6 10
3 ? 11
4 8 12
Now, read the numbers from left, top to bottom. The missing number is obviously 7.
1 + 9 + 8 = ?
considering, 28 + 8 + 92 = 10
10
br>Equation 28 + 8 + 92 = 10 can be derived from
twenty eight(t) + eight(e) + ninetytwo (n) = ten => 10
Similarly for equation,
1 + 9 + 8
One (o) + nine (n) + eight (e) => one (1)
There are many trees in my garden. One such tree is a mango tree and obviously, there are some mangoes on it. Using the Slingshot I try to get some mangoes. After half an hour there are no mangoes on trees and no mangoes with me.
How come ?
There are two mangoes on the tree. Using Slingshot I got one mango.
Therefore now one mango is with me and one mango is in the tree (note: we do not have mangoes (plural of mango).
Can you solve the equation by finding the value ofA) HorseB) Cowboy bootC) Horseshoe
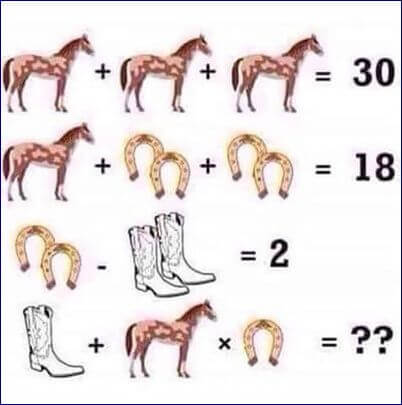
Horse = 10, Cowboy-Boot = 1 ,HorseShoe= 2
= Step1 =
3Horse = 30
=> Horse = 10 .....(A)
= Step2 =
1Horse + 2HorseShoe + 2HorseShoe = 18
10 + 4HorseShoe =18
HorseShoe = 2 .....(C)
= Step3 =
2HorseShoe - 2Cowboy-Boot = 2
4 - 2Cowboy-Boot = 2
=> Cowboy-Boot = 1 ... (B)
= Step4 =
Cowboy-Boot+Horse*HorseShoe = 1+10*2 =>21