Yahoo Interview Puzzles Questions With Answers | Best Riddles and Brain Teasers

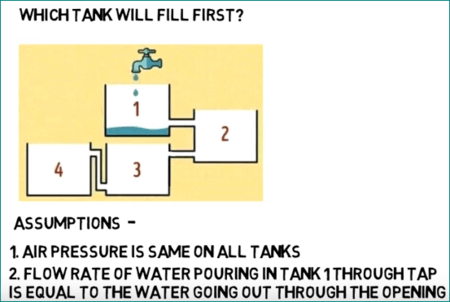
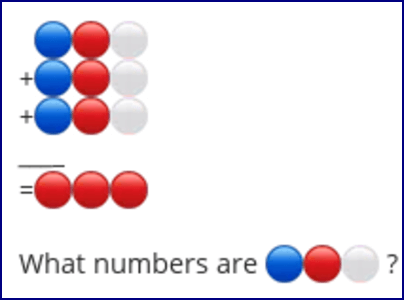
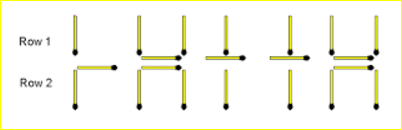
#131 - Hard Prison CupCakes Riddle

Bea Smith , Vera Bennett, Franky Doyle and Doreen Anderson were in Wentworth Prison for murder. But their behavior on the jails is appreciated by the warden and the warden decided to give all these 4 prisoners 11 cupcakes.They all like cupcakes and they had all cupcakes in no matter of time but they do not know how many cupcake each individual had.Therefore Bea started the conversation Bea : "Hey T-Vera, did you had more cupcakes than I had ?"Vera : "I do not know girl, Hey Franky, did you had more cupcakes than I had ?".Franky: "I do not know"Doreen replied instantlyDoreen: "I know how exactly how many cupcakes each of you had?"So can you tell how many cupcakes each of them had ?

View Answer Discuss

Bea : 1 cupcake
Vera : 2 cupcakes
Franky: 3 cupcakes
Doreen : 5 cupcakes

It is obvious if the prisoner person has eaten five or more of cupcakes than she wound not raise this question "did you had more cupcakes than me?" because it will make her the one who had eaten most cupcakes.

* Bea must do not have eater 5 cupcakes, therefore she has eaten anywhere between 1-4 cupcakes.
* Since Bea asked her the question Vera knows the fact that Bea has eaten 1-4 cupcakes and based on Vera reply, it is obvious she has eaten 2-4 cupcakes.
* Franky knows Vera replied with the answer as "I do not know and based on above logic, she must have had 3 or 4 cupcakes.
* Doreen replied she know all, which indicates she must have eaten 5.

#132 - Square Root 12345678987654321 Puzzle

The square root of number 121 is "11". What is the square root of number "12345678987654321." ?

View Answer Discuss

111111111

It is a very popular square root series i.e.
Square root fo number 121 is 11
Square root fo number 12321 is 111
Square root fo number 1234321 is 1111 and so on....

#133 - Fill The Tank Riddle

Which tank will fill first?

View Answer Discuss

3rd and 4th.Let us break down the problem into 5 steps.1. The water in tank1 will get filled up to the connectivity of tank1 and the tank2 and then it will start flowing to tank2.2. The water in tank2 will get filled up to the connectivity of tank2 and the -tank3 and then it will start flowing to tank3.3. The water in tank3 will get filled up to the connectivity of tank2 and the tank3 and then it will start flowing to tank3.4. As the outlet of tank3 and inlet of tank4 are not at the same level, water will continue to fill tank3 till the inlet of tank4.5. Now both the tank3 and tank4 fill simultaneously until both fill together.

#134 - The Cards Magic Riddle

David Blaine and Dynamo performed together in our college fest. I was chosen to be performed a card trick on. Blaine asked me to shuffle a deck of cards and when I was done, he asked me to pick any five cards. I did as he had asked and showed my selected cards to Blaine. Out of those five cards, he gave four to Dynamo and one back to me. Upon looking at those four cards, he was able to deduce the card I was holding. I was shocked. It was brilliant. But when I was returning back home, I thought about it and was able to crack the trick. Do you know how they did it?

View Answer Discuss

It is plain and simple that in five cards, two cards must be of the same suit.

What Blaine did was place one of those cards at the end and gave the other cards to Dynamo. Now, Dynamo knows the suit of the card.

So how did Blaine ensure that Dynamo knows the number on the card as well?

Since one of the cards determines the suit, we have 3 cards. If you know a little about permutations, the 3 cards can be arranged in 3! ways i.e. 6 ways. If we make sure that the King is not picked, it leaves us with just 12 numbers.

The cards can be distinguished from upside down position, which gives us 6*2 ways of arranging the cards.

Let us denote the smallest card as X1U for upward position and X1D for the downward position. We can go up from there as X2U, X2D, X3U, X3D and so on.

The possible 12 arrangements will now be
X1U X2U X3U => Card No. 1
X1U X3U X2U => Card No. 2
X2U X1U X3U => Card No. 3
X2U X3U X1U => Card No. 4
X3U X1U X2U => Card No. 5
X3U X2U X1U => Card No. 6
X1D X2D X3D => Card No. 7
X1D X3D X2D => Card No. 8
X2D X1D X3D => Card No. 9
X2D X3D X1D => Card No. 10
X3D X1D X2D => Card No. 11
X3D X2D X1D => Card No. 12

#135 - Number Dot Algebric Riddle

Can you solve the below algebraic picture puzzle?

View Answer Discuss

1 8 and 5 (185+185+185 = 555)

#136 - Minutes Feb 2017 Riddle

How many minutes are there in Feb 2017?

Note: Shortest answer is the correct answer.

View Answer Discuss

8! minutes (28 days x 24 hours x 60 minutes = 40,320 = 8! minutes)

#137 - King Four Rooks Riddle

You are playing as white and given four rooks to checkmate the black king in four moves with following rules.1. You can place one rook every move and ensure black king should be in check position.2. After four moves the black king should be in the checkmate position.

View Answer Discuss

Four moves are shown in the picture below.

#138 - Ant And Rope Riddle

An ant is traveling on a 1meter long rope at 1cm/seconds but also the entire rope is being stretched by an extra 1meter/second.Is it possible for the ant to reach at the end of the rope?

View Answer Discuss

Yes as once the ant moves the rope behind the ant also stretches and therefore will be accounted as well.

#139 - Cipher Matchsticks Riddle

Can you decipher the two rows to find the hidden word?

View Answer Discuss

Flip the two rows 1 and 2 vertically, you will find the word "Lotto".

#140 - Classic Philosophical Betrayed Riddle

John and Sophie were so frustrated with their life that they decided to end the misery by ending their life. They decided that both will jump off the building on the count of three. They started counting and on the count of three, John jumped white Sophie did not. She watched John fall off for around seven seconds when the parachute opens.

Who betrayed whom?

View Answer Discuss

John betrayed Sophie.
Sophie may not jump because of the survival instinct and therefore can be given a benefit of the doubt, whereas John having the parachute seem a well-thought plan.