#411 - Fun But Hard Maths Riddle
How high will you have to count before you use the letter A?
One Thousand
#412 - Mathematical Logical Puzzle
Consider the situation that there is a pond where some flowers have grown up and some bees are hovering over the flowers. Now read the following statements carefully:
1. If each of the bees lands on a flower, then one bee does not get a flower.
2. If two bees share each flower, then there is one flower left.
Now, can you calculate the number of flowers in the pong and the number of bees hovering over them?
There are three flowers in the pond and four bees are hovering over it.
#413 - worlds trickiest riddle
The doctor prescribed you to take one pill from the bottle every half an hour. The bottle is now left with only three pills.
How long do you think you have before you run out of pills?
You have an hour.
The most common answer will be one and a half hour. But remember, when you took the first pill, it was the zero minute.
#414 - Engineer Riddle
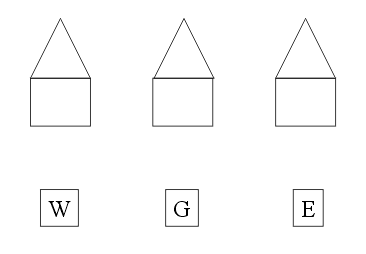
Look at the figure below. You have three house and there are three utilities below it: W representing water, G representing gas and E representing Electricity. You have to draw a line that gets each utility into every house without crossing the lines. Can you do it?
This puzzle is known as the Turan Brickyard Problem and is a classic one. There is no way that they can be connected without crossing the lines in 2 dimension. However, you can do it if you place the scene in a 3d workplace. See to the figure to understand better.
#415 - Hard Conditional Probability Problem
Four friends - Anna, Brian, Christy and Drake are asked to choose any number between 1 and 5.
Can you calculate the probability that any of them chose the same number ?
Let us take this one step at a time.
Let us calculate the probability that Anna and Brian have the same number in their mind.
101/125
Now, there's a 1/5 chance that the numbers will be same and 4/5 chance that the numbers are different.
Let us now include Christy in this data. There can be two cases.
1) Anna and Brian have the same number. In that case, Christy will have only one number to compare.
2) Anna and Brian did not have the same number. In that case, Christy will have two numbers to compare to.
For the first case, the probability will be 5/25. This is if Anna and Brian did have the same numbers.
But if Anna and Brian did not have the same numbers, there is a 2/5 probability that Christy is having the same number (this is because Christy gets to match her number with both Anna and Brian). In that case, we can simply multiply the probabilities.
4/5 * 2/5 = 8/25
Otherwise, if Christy is not having the same number, the probability is 3/5. Now multiplying with the previous chain:
4/5 * 3/5 = 12/25
Now, we can include Drake in our calculations. If we follow the path where Drake's number matches with Anna and Brian, the probability will be 25/125.
Now let us join that with Christy's probability. If Christy's number matches with Anna and Brian and Drakes' number also matches, then the probability will be:
4/5 * 2/5 = 40/125
If Christy's number does not match with Anna and Brian but Drake's number matches with Christy's, the probability will be:
4/5 * 3/5 * 3/5 = 36/125
But if Christy's number does not matches with Anna and Brian and even Drake's does not matches with Christy, then the probability will be:
4/5 * 3/5 * 2/5 = 24/125
Now, we have to tell the probability when all the four friends have same numbers, so we will just add up the probability where all the numbers matches:
25/125 + 40/125 + 36/125 = 101/125.
#416 - What Word Am I Thinking Of Riddle
I am an eleven letter word.
The first, second, third and fourth letter combine to form a bankquot;s name.
The fifth, sixth and seventh letter combine to form a carquot;s name.
The eighth, ninth, tenth and eleventh letter combine to form a mode of transport.
Can you identify what word am I?
CITIZENSHIP
#417 - Cricket Riddle
How many runs at maximum can a batsman score in a normal one day match? Consider the fact that the conditions are ideal and there are no No Balls, no Wide Balls and no Extras in that match.
If we are considering an ideal case and we have to calculate the maximum score, we will assume that the batsman hits six on every ball. But then, at the end of every over, the strike will change. But we have to make sure, he gets to play maximum number of balls to score maximum runs. Thus, the batsman will hit six in first five balls and will choose to take 3 runs in the last ball so that he retains the strike in the following over.
Total runs per over in that case = 6 * 5 + 3 = 33.
But in the last over (50th over), he don’t have to worry about keeping the strike and thus, he will hit six even on the last ball. Therefore, the maximum runs that a batsman can score:
33 * 49 + 6 * 6 = 1617 + 36 = 1653
#418 - Mystery Number Riddle
Consider all the numbers between 1 and 1 million. Among all these numbers, there is something very special about the number 8 and the number 2202. What is it ?
If you start arranging the numbers alphabetically, the numbers 8 (eight) will come first and the number 2202 (two thousand two hundred and two) will come at last.
#419 - Fun Probability Question
Upon tossing a fair coin ten times, you get heads every time.
What is the probability that in the next toss, it will land with heads up again?
50%
The next toss of the coin is not dependent upon the previous ten tosses. Thus, the probability is 50 percent only.
#420 - Tricky Number Sequence Puzzle
Analyze and find the missing item in the sequence:
16, 06, 68, 88, __, 98
L8
This is a bit tricky questions. To solve you must look at the series upside down. It is actually
91, 90, 89, 88, __, 86
So we need 87 in the place of blank. To achieve 87 in an upside down position, the correct answer will be L8.
Thus, the missing item in the series is L8.