#71 - Algebra Maths Equation Riddle
Can you solve the below algebraic mathematical equation?
(J+O+I+N+T)3 = JOINT
(1+9+6+8+3)*(1+9+6+8+3)*(1+9+6+8+3) = 19683
J = 1, O = 9, I = 6, N = 8, T = 3
#72 - Good Equation Riddle
Is it possible to get ten whether you remove one from nine or eleven? How?
It is possible if you write numbers in their roman forms.
11 = XI
If I (1) is removed, it becomes X = 10
9 = IX
If I (1) is removed, it becomes X = 10
#73 - Trick Maths Equation Problem
The following question it puts forth you:
25 - 55 + (85 + 65) = ?
Then, you are told that even though you might think its wrong, the correct answer is actually 5!
Whats your reaction to it? How can this be true?
If you read the question again, you will probably notice the slight trick used in this question.
25 - 55 + (85 + 65) = 25 - 55 + 150 = 120
Now, 120 is also equal to 5!
5! = 5 * 4 * 3 * 2 * 1 = 120
Yes, we were talking about 5! (factorial) and if you read the question, thats what is written there.
#74 - Statement Equation Riddle
A + B = C
D - C = A
E - B = C
Based on the above equations, can you find out the outcome for:
D + F ?
In this question, the alphabets represent their equivalent numeric position.
A = 1, B = 2, C = 3 and so on.
Thus,
A + B = c
=> 1 + 2 = 3
D - C = A
=> 4 - 3 = 1
E - B = C
=> 5 - 2 = 3
Which is why,
D + F = 4 + 6 = 10
Since, J is the 10th alphabet,
D + F = J.
#75 - Popular Algebraic Equation Riddle
Can you solve the popular algebraic equation by replacing alphabets with a digit and equation must be true as well?
SEND
+ MORE
======
MONEY
9567
+ 1085
======
10652
#76 - Toothpick Equation Riddle
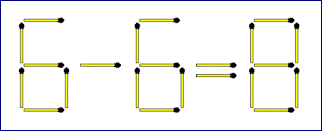
By moving just one toothpick(matchstick), you need to make below statement true.Can you do it?
Check solution in image below.
#77 - Correct Matchsticks Equation
Remove two matchsticks to make below statement true.
Solution is solved below.
#78 - Use Symbols Make Equation
Using the mathematical symbols like +, -, and x in order to make the equations correct. Replace @ with the above given symbols.
9 @ 8 @ 7 @ 6 @ 5 @ 4 =91
9 x 8 - 7 + 6 x 5 - 4 = 91
#79 - Fill The Numbers Puzzle
Given below is a figure. You have to fill in the numbers from 1 up to 16 in such a way that you get 29 when you add the numbers in each row.
Solution is explained in picture below
#80 - Create Function Puzzle
There are two variables x and y. Jimmy is required to construct a function f(a,b) which returns the maximum one in {a,b}.
You can only use +,-,ยท, / & abs() (to take the absolute value). NO if () is allowed in to jimmy.
Solve this one, math freaks.
{a+b+abs(a-b)}/2
Also, {a+b-abs(a-b)}/2 is the smaller one in {a,b}