#81 - Algebra Riddle
Solve the equation by replacing alphabet with number.
MOM + MOM + NO = BOOK=
757+757+45=1559
#82 - Algebra MCQ Puzzle
ENEMY = 2 * LINK
LINK + 2 = HELL
Then what will be TAXI + HELL? Select from the options below:
a) ROTTEN
b) DANGER
c) HEAVEN
4) MORTAL
The answer is HEAVEN.
ENEMY = 4 + 3 + 4 + 4 + 3 = 18
LINK = 2 + 1 + 3 + 3 = 9
HELL = 3 + 4 + 2 + 2 = 11
TAXI = 2 + 3 + 2 + 1 = 8
HEAVEN = 3 + 4 + 3 + 2 + 4 + 3 = 19
Therefore, TAXI + HELL = 8 + 11 = 19 = HEAVEN.
#83 - Letter To Number Puzzle
In the figure that has been attached with this question, each digit represents a digit. The similar letters carry the same integer value.Can you expose the original digits?
See the picture for the answer. T = 1W = 3O = 8H = 9R = 0E = 4
#84 - Mathematical Symbols Riddle
Can you make the number 24 by utilizing the numbers 1, 3, 4 and 6? You must use one number only one time and you can use mathematical operation symbols anytime anywhere.
6/(1 - 3/4) = 24
#85 - Brain Twist Math Equation
Can you write a mathematical expression having a value of twenty four, that uses three equal digits, none of them being eight.
22 + 2 = 24
#86 - 8 Number Grid Puzzle
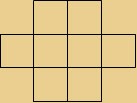
You are provided with a grid (as shown in the picture). Can you fill the squares with numbers 1-8 in a manner that none of the two consecutive numbers are placed next to each other in any direction (vertically, horizontally or diagonally?)
This problem can be solved in four different ways. The picture shows you one of the solutions. Can you find out the other three?
#87 - Complete The Equation Puzzle
Below, you can see three complete equations and one incomplete. Based on the three complete ones, can you complete the incomplete one?
5 $ 4 $ 3 $ 9 = 4215
6 $ 9 $ 2 $ 6 = 3816
4 $ 7 $ 3 $ 3 = 1122
7 $ 2 $ 7 $ 4 = ____
2418 is the answer.
The algo that has been used here is
A $ B $ C $ D = [first digit of (A * D)] [last digit of (B * C)] [first digit of (B * C)] [last digit of (A * D)]
Using the same algo,
7 $ 2 $ 7 $ 4 = [first digit of (7 * 4)] [last digit of (2 * 7)] [first digit of (2 * 7)] [last digit of (7 * 4)]
= 2418
#88 - Matchstick Equation Puzzle
An equation has been laid down using a few matchsticks. However, as you can see, the equation is not correct. Can you correct the equation if you are allowed to add or remove 5 matchsticks?
As you can see in the answer figure, the equation stands true now. Compare the images to know what we have done.
#89 - Mathematical Proof Puzzle
Below, you will find the mathematical proof that 10 equals 9.99999…. But is that possible or there is something wrong about it? Can you find the error?
x = 9.999999...
10x = 99.999999...
10x - x = 90
9x = 90
x = 10
No error is present in this proof and 10 is actually equal to 9.99999…. The proof is absolutely correct.
#90 - Math Algebra Equation Problem
Can you find out the value of x in the following equation?
(2^x) (30^3) = (2^3) (3^3) (4^3) (5^3)
(2^x)(30^3) = (2^3) (3^3) (4^3) (5^3)
(2^x)(30^3) = (120^3)
(2^x) = (120^3)/ (30^3)
(2^x) = (4^3)
(2^x) = 64
ln(2^x) = ln(64)
x ln(2) = ln(64)
x = ln(64)/ln(2)
x = 6
Thus x = 6.