In a rectangular garden, a sneaky snake is slithering swiftly along the length. Simultaneously, a determined man begins his pursuit from one end of the breadth. The snake moves at a steady pace of 30 cm/hour, while the man walks twice as fast, covering 60 cm/hour.
The question is, how long will it take for the man to catch up to the snake?
Consider the garden's breadth as "B" and its length as "2B." The man and snake start moving at the same time.
To find the time "T" when the man catches the snake, we equate the distances they both cover.
Man's distance: 60T (60 cm/hour * T hours)
Snake's distance: 30T (30 cm/hour * T hours)
The man catches the snake when they meet at the same point, meaning the distance covered by both is equal.
Equation: 60T = 30T
Solving for "T":
60T - 30T = 0
30T = 0
T = 2
Thus, the man catches the snake after 2 hours.
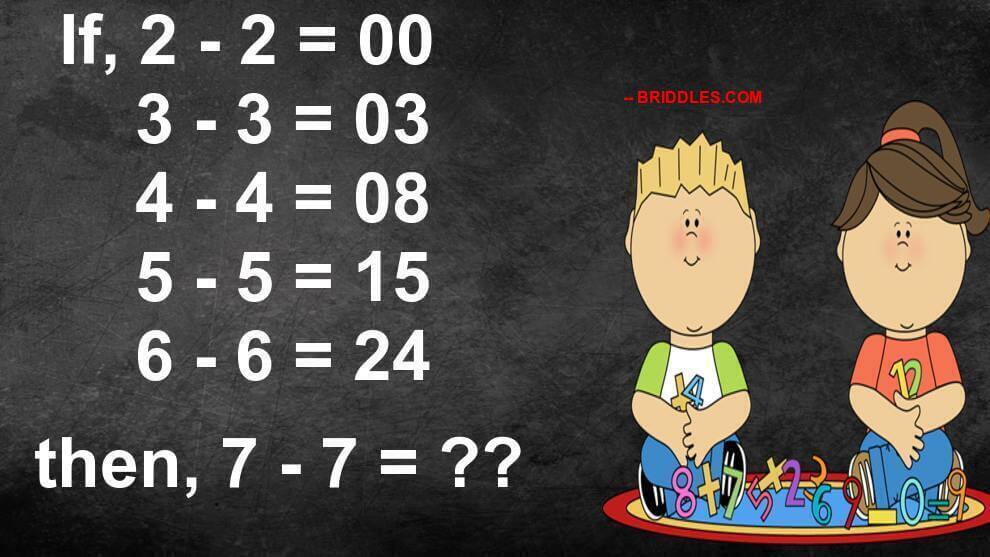

-Viral-Maths-Puzzle-2215.jpeg)
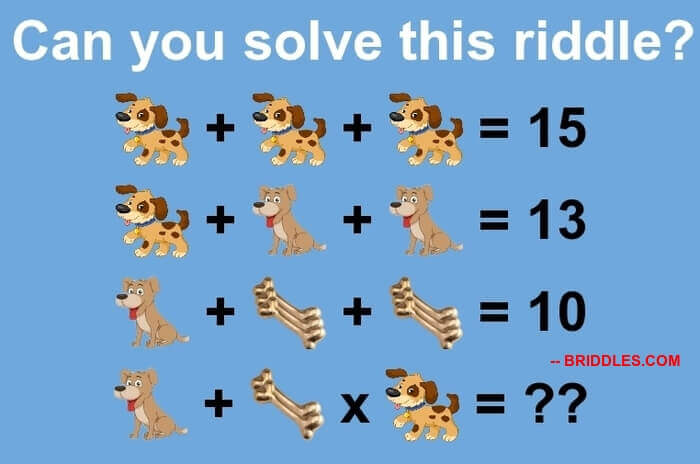

^3-x-4-divide-2-Maths-Equation-2255.jpeg)