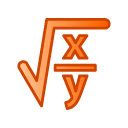#181 - Maths Riddle

There is one four-digit whole number n, such that the last four digits of n2 are in fact the original number n

View Answer Discuss

Looking at the last digit, the last digit must be either 0, 1, 5 or 6.
Then looking at the last two digits, the last two digits must be either 00, 01, 25 or 76.
Then looking at the last three digits, the last three digits must be either 000, 001, 625 or 376.
Then looking at the last four digits, the last four digits must be either 0000, 0001, 0625 or 9376.
Out of those, only 9376 is a 4 digit number

#182 - November Puzzle

In the addition below, all digits have been replaced by letters. Equal letters represent equal digits and different letters represent different digits.
ABCABA
BBDCAA
ABEABB
ABDBAA
------- +
AAFGBDH
What does the complete addition look like in digits?

View Answer Discuss

The complete addition looks as follows:
167161
664711
162166
164611
------- +
1158649

#183 - Maths Puzzle

How can I get the answer 24 by only using the numbers 8,8,3,3.

You can use the main signs add, subtract multiply and divide.

Maths Puzzle
View Answer Discuss

1) 8/(3-(8/3))
= 8/(1/3)
= 24

2)((8 x 3!)/3)+8
= ((8 × 3 × 2 × 1)/3)+8
= (48/3)+8
= (16)+8
= 24

3)(3!/)*8

4)(8-3)!/(8-3)
( × )!
( + )!
√(8×8×3×3)
8+(8×(3!/3))
((√(8+8) × (3/3))!
√(8+8) × (3+3)
(log base(3!/3) of 8) × 8
((log base(3!/3) of (8+8))!

#184 - Math Puzzle

You have 1023 apples and 10 bags. You have to distribute these lemons in these 10 bags in any way you choose. But when I ask for a certain number of lemons you have to give them in terms of bags without transferring the lemons from other bags. How do you distribute the lemons?

Math Puzzle
View Answer Discuss

Starting with 1 apple in a bag, each bag contains double the number of apples as the previous bag. ie 1,2,4,8,16,32,64,128,256,512. That way whatever number of apples I would ask for you would just add up the bags to equal the number asked.

#185 - Sam Loyd Maths Puzzle

Charley Smalleash treats his best girl to a trolley ride, but on account of his limited resources they plan to walk back, so, if the car goes at the rate of nine miles an hour and they can walk at the rate of three miles an hour, how far could they ride if they must be back in eight hours?

Sam Loyd Maths Puzzle
View Answer Discuss

Charley Smalleash and his best girl could trolley three times as fast as they could walk. Therefore, three-quarters of their outing time was spent in walking, and but one-quarter in riding, since they had to walk back.

They rode for two hours, going 18 miles, and walked back in six hours, thus consuming their eight hours.

#186 - Tricky Nine Maths Riddle

A new medical building containing 100 offices had just been completed. Mark was hired to paint the numbers 1 to 100 on the doors. How many times will Mark have to paint the number nine?

Tricky Nine Maths Riddle
View Answer Discuss

The correct answer is twenty (9,19,29,39,49,59,69,79,89,90,91,92,93,94,95,96,97,98,99(2) and so on).

#187 - Mathematical Riddle

Using only two 2's and any combination of mathematical signs, symbols and functions can you make 5?

Mathematical Riddle
View Answer Discuss

SQRT(.2 ^ -2)
Take .2 and raise it to the power of -2 and then take the square root.

#188 - February Series Question

Find The Next Number
12 13 15 17 111 113 117 119 123 ?

February Series Question
View Answer Discuss

129.

These are the first 10 prime numbers (2, 3, 5...) prefixed with a 1

#189 - Maths Quiz

Fred can eat 27 chocolates in a hour, Alice can eat 2 chocolates in 10 minutes, and Kelly can eat 7 chocolates in 20 minutes. How long will it take them to share and eat a large box of 120 chocolates whilst watching a movie?

Maths Quiz
View Answer Discuss

2 hours.

In one hour, Fred eats 27 chocolates, Alice eats 12, and Kelly eats 21. A total of 60 chocolates. Therefore 120 chocolates would take 120 ÷ 60 = 2 hours. QED.

#190 - Answer a Maths Riddle

Can you find a seven digit number which describes itself. The first digit is the number of zeros in the number. The second digit is the number of ones in the number, etc. For example, in the number 21200, there are 2 zeros, 1 one, 2 twos, 0 threes and 0 fours.

View Answer Discuss

3211000